Logaritmii
log xy = log x + log y
Ce spun ?
Cum se inmultesc numerele,nu prin operatia de inmultire, ci prin adunarea unor numere asociate.
De ce este important ?
Adunarea este mult mai simpla decat inmultirea.
La ce au condus?
Metode eficiente pentru calculul fenomenelor astronomice cum ar fi eclipsele si orbitele planetelor. Moduri rapide de efectuare a calculelor stiiin tifice.Partenerul credincios al inginerului,rigla de calcul.Dezintegrarea radioactiva si psihofizica perceptiei umane.
Numerele isi au originea in probleme practice:consemnarea proprietatilor, cum ar fi animalele sau terenurile si a tranzactiilor financiare, cum ar fi impozitele si tinerea contabilitatii. Cea mai veche notare a numerelor, in afara semnelor pe raboj de genul IIII, se gaseste pe exteriorul plicurilor din lut.In anul 8 000 I.Hr.,contabilii din Mesopotamia tineau registre folosind tablite din lut de diferite forme.
Arheologul Denise Schmandt-Besserat si-a dat seama ca fiecare forma reprezinta o marfa de baza – o sfera pentru grane, un ou pentru un vas de ulei si asa mai departe.Din motive de siguranta,aceste marturii scrise erau sigilate in invelitori din lut.Dar era complicat sa spargi o invelitoare din lut ca sa afli cate marturii erau inchise inauntru, asa ca acesti contabili ai Antichitatii zgariau simboluri pe exteriorul invelitorilor pentru a indica ce se afla inauntru.In cele din urma, si-au dat seama ca, avand aceste simboluri,puteau sa inscriptioneze marturiile.Rezultatul a fost o serie de simboluri scrise pentru numere-originea tuturor celorlalte simboluri numerice ulterioare si,posibil,chiar a scrisului.
Odata cu numerele,a aparut si aritmetica:metode de adunare,scadere,inmultirea si impartirea numerelor.Pentru adunare au fost folosite dispozitive cum ar fi abacul;pe urma, rezultatele puteau fi consemnate prin simboluri.Dupa un timp,au fost gasite caile pentru folosirea simbolurilor fara sa mai fie necesara asistenta mecanica,desi abacul este folosit in continuare la scara larga in multe colturi ale lumii in vreme ce calculatoarele electronice au inlocuit calculele cu creionul pe hartie in majoritatea celorlalte tari.
Aritmetica s-a dovedit a fi esentiala si din alte puncte de vedere, in special in astronomie si topografie.Pe masura ce au inceput sa apara elementele de baza ale stiintelor fizice,oamenii de stiinta novici au fost obligati sa efectueze calcule si mai complicate, cu mana.Adeseori acestea le ocupau cea mai mare parte a timpului, uneori luni sau ani intregi,afectandu-le activitatile mai creative. In cele din urma,accelerarea procesului a devenit esentiala.au fost inventate nenumarate dispozitive mecanice,dar pasul cel mai important a fost unul conceptual:gandeste mai intai si calculeaza pe urma. Folosindu-se de matematica inteligenta,calcule dificile puteau fi efectuate cu mult mai usor.
Noua matematica a capatat curand o viata proprie,dovedindu-se a avea implicatii profunde atat teoretice,cat si practice. In zilele noastre,aceste idei timpurii au devenit un instrument indispensabil pentru stiinta in ansamblul ei,ajungand pana si in psihologie si in stiintele umaniste.au fost larg utilizate pana in anii 1980,cand computerele le-au facut desuete pentru scopurile practice,dar,in ciuda acestui fapt,importanta lor pentru matematica si stiinta a continuat sa creasca.
Ideea de baza este o tehnica matematica numita logaritm.Inventatorul ei este un lord scotian,insa a fost nevoie de un profesor de geometrie,deosebit de preocupat de navigatie si astronomie,pentru inlocuirea ideii stralucite, dar incomplete a mosierului, cu una mult mai buna.
In luna martie 1615, Henry Briggs I-a trimis o scrisoare a lui James Usser, in care este consemnat un eveniment crucial in istoria stiintei:
” Nappre, lord de Markinston,mi-a pus mainile si capul la munca cu noii si admirabilii logaritmi. Sper sa-l vad in aceasta vara,daca este voia lui Dumnezeu ,caci nu am vazut niciodata o carte care sa-mi faca mai multa placere sau care sa ma faca sa ma minunez mai mult.”
Briggs a fost primul profesor de geometrie de la Colegiul Gresham din Londra iar “Napper, lord de Markinston” a fost John Napier, al optulea lord de Merchiston,mosie care actalmente face parte din orasul Edinburgh din Scotia.Napier pare sa fi fost cam mistic;avea preocupari teologice deosebite,dar acestea se concentrau mai mult asupra Apocalipsei. Din punctul lui de vedere, cea mai importanta lucrare apartinandu-i a fost A Plaine Discovery of the Whole Revelation of St. John – Dezvaluire limpede a revelatiei Sfantului Ioan in intregul ei, care l-a condus la anticiparea sfarsitului lumii ori in 1688,ori in 1700.Se crede ca se ocupa atat de alchimie,cat si de necromatie si preocuparile sale legate de ocultism I-au conferit reputatia de magician.Potrivit zvonurilor,purta la el un paianjen negru intr-o cutie mica oriunde s-ar fi dus si avea companion ”familiar” sau magic:un cocos negru.
Potrivit unuia dintre descendentii lui, Mark Napier, John isi folosea companionul familiar pentru a-i prinde pe servitorii care furau.Ii inchidea pe suspecti intr-o incapere cu cocosul si le dadea instructiuni sa ii mangaie,spunandu-le ca pasarea vrajita putea sa-l detecteze pe vinovat fara gres.Insa misticismul lui Napier avea un miez rational,care in aceasta imprejurare particulara presupunea acoperirea cocoselului cu un strat subtire de negru fum.Servitorul nevinovat avea toata increderea sa mangaie pasarea potrivit instructiunilor si s-ar fi murdarit pe maini.Unul vinovat,temandu-se sa nu fie dovedit,ar fi evitat sa mangaie pasarea.Si astfel,in mod ironic,mainile curate dovedeau vinovatia.
Napier si-a dedicat mare parte din timp matematicii si in special metodelor de iutire a rezolvarii calculelor matematice complicate.Una din inventiile lui, riglele lui Napier, era constituita din zece riglete pe care erau marcate numere,care simplificau procesul inmultirilor lungi.Si mai valoroasa a fost inventia care i-a conferit reputatie si a creat o revolutie stiintifica: nu a sa carte despre Apocalipsa, cum sperase, ci alta, intitulata Mirificii Logarithmorum Canonis Descriptio -Descrierea minunatului canon al logaritmilor, din anul 1614.Prefata arata ca Napier a stiut exact ce descoperise si la ce anume era utila inventia lui.
In momentul in care a aflat de logaritmi, Briggs a fost incantat. Asemenea multor matematicieni din epoca sa, petrecuse foarte mult timp efectuand calcule astronomice.Stim acest lucru deoarece intr-o alta scrisoare trimisa de Briggs lui Usser,datata din 1610, se mentioneaza calcularea eclipselor si pentru ca Briggs publicase anterior doua carti de tabele numerice,unul avand legatura cu Polul Nord si celalalt cu navigatia.Toate aceste lucrari ii impusesera un volum mare de calcule complicate,aritmetice si trigonometrice.Inventia lui Napier putea sa scuteasca de o foarte mare parte de munca plictisitoare.Dar cu cat a studiat mai mult cartea,cu atat Briggs a venit cu o imbunatatire simpla,dar eficienta si a facut o calatorie lunga, pana in Scotia.Cand s-au aflat fata in fata, “aproape un sfert de ora s-a scurs,fiecare privindu-l pierdut in admiratie pe celalalt,inainte sa se rosteasca vreun cuvant”.
Ce anume a provocat o asemenea admiratie ? Observatia vitala,evidenta pentru oricine invata aritmetica, era ca adunarea numerelor este relativ simpla,insa inmultirea nu. Inmultirea cere mai multe operatii aritmetice decat adunarea. De exemplu adunarea a doua numere de cate zece cifre presupune zece pasi simpli, insa inmultirea necesita 200. Chiar si pentru computerele moderne e o problema importanta dar este ascunsa in culise, in algoritmii folositi pentru inmultire.
Briggs a identificat aceasta problema si si-a dat seama cum sa o rezolve: sa foloseasca o baza putin mai mare decat 1. De asemenea, a sesizat si o problema mai subtila si s-a ocupat si de ea. Daca metoda lui Napier ar fi fost modificata sa fie aplicabila pentru valorile puterilor unui numar de genul 1,0000000001, nu ar fi existat nicio legatura directa intre logaritmii numerelor 12,3456 si 1,23456.Prin urmare,nu era prea clar unde putea sa se opreasca tabelul. Sursa problemei era valoarea pentru log 10, pentru ca:
Log 10x = log 10 + log x
Si asa a inceput istoria logaritmului in baza 10.
Daca ti-a placut acest articol, daca doresti sa afli mai multe despre cursurile de dezvoltare personala si meditatii la matematica , cum te pot ajuta si de ce sunt utile , astept un mesaj pe email.:contact@meditatii.eu.
Inscrie-te la newsletter, vei primi informatii utile si oferte speciale, dedicate numai celor care se aboneaza.
„Citat din: 17 ecuatii care au schimbat lumea de Ian Stewart”


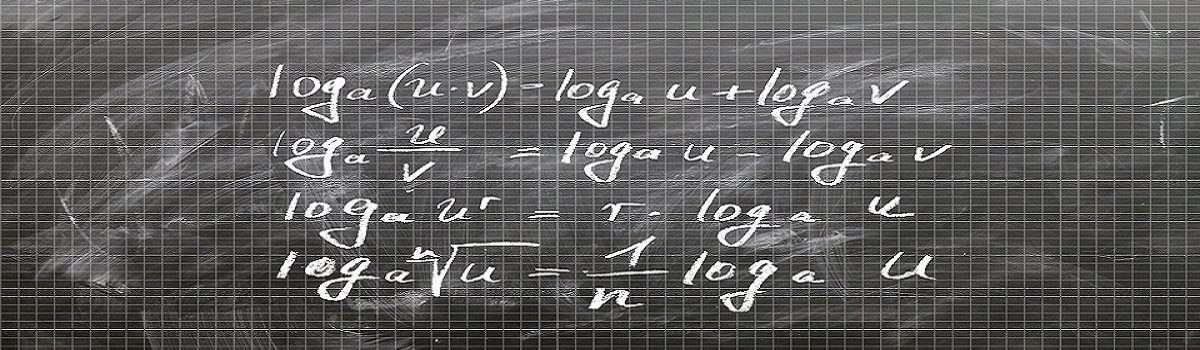



Comentarii recente